

II. Тензоры. 2.3. Свойства симметричного тензора II валентности
Для симметричного тензора имеет место соотношение
| b × (S × a) = a × (S × b) | (28) |
Действительно,
| B × (S × a) = bk (Sk i ai) = bk Si k ai = ai Si k bk = a × (S × b). |
Геометрическая интерпретация
Симметричные тензоры допускают некоторую геометрическую интерпретацию. Начнем с того, что вектор
a можно представить не только направленным отрезком, но и плоскостью
| a × r = 1, | (29) |
где
r – радиус-вектор произвольной точки, принадлежащей этой плоскости. Это ясно из того, что| a × r = a × ra = 1, a × (r – ra) = 0; | (30) |
длина
ra – векторной проекции радиус-вектора r на вектор a равна 1/a; все векторы r – ra перпендикулярны вектору a, т. к. равно нулю их скалярное произведение с a; таким образом, все векторы r – ra принадлежат плоскости, перпендикулярной вектору a и проходящей через конец вектора ra. На прямой, проходящей через начало координат и имеющей направление вектора a, плоскость, определяемая уравнением (28), отсекает отрезок длины r = 1/a.Аналогичное рассмотрение проведем для симметричного тензора
S. Рассмотрим поверхность, определяемую уравнением| r × (S × r) = 1, | (31) |
где
r – радиус-вектор произвольной точки, принадлежащей этой поверхности. Распишем это уравнение в координатах:|
| (32) |
В этом соотношении нетрудно увидеть поверхность второго порядка. Т. к. уравнение (31) не связано с конкретной системой координат, при повороте, сдвиге или отражении координатной системы вид поверхности не изменится.
Найдем точки пересечения этой поверхности с координатными осями. На оси
OX1 x2 = x3 = 0, так что из формулы (32) получаем|
| (33) |
Если
S11< 0, в формулах (31) и (32) правую часть следует приравнять – 1, тогда под корнем выражения (33) будет положительная величина – S11. К аналогичным результатам придем для других координатных осей, поскольку на оси OX2 x3 = x1 = 0, и на оси OX3 x1 = x2 = 0:
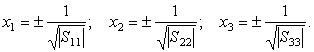
| (34) |
Если
S11, S22 и S33 имеют одинаковый знак – случай, весьма важный для приложений, – поверхность (31) будет поверхностью эллипсоида. Она и является геометрическим образом симметричного тензора второй валентности в пространстве трех измерений, подобно тому как плоскость дает геометрический образ тензора валентности 1, т. е. вектора. Поэтому уравнение (32) называется уравнением тензорного эллипсоида, хотя оно может описывать и другие поверхности второго порядка.При преобразованиях координат компоненты тензора изменяются по формулам (8), однако сам эллипсоид от выбора системы координат не зависит. Пусть имеется некоторая штрихованная система координат. В ней расстояние от начала координат до точки
M поверхности тензорного эллипсоида, пересекаемой осью X¢ , равно в соответствии с формулой (33)
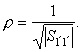
|
В нештрихованной системе это же расстояние с учетом формулы (8) представится в виде
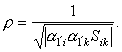
|
Другими словами,
r есть расстояние от начала координат то поверхности тензорного эллипсоида в направлении, задаваемом направляющими косинусами a1¢ 1, a2¢ 1, a3¢ 1.Нормаль к касательной плоскости
Простое геометрическое значение имеет
S × r: если точка M c радиус-вектором r принадлежит поверхности, описываемой уравнением (31), то вектор| b = S × r | (35) |
имеет направление нормали к плоскости, касательной к поверхности в точке
M. Чтобы убедиться в этом, сместим точку M на dr так, чтобы она оставалась на поверхности.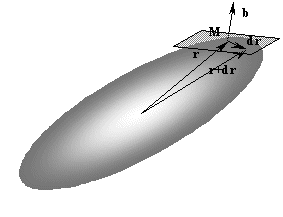
Ее новым радиус-вектором будет
r + dr. Очевидно, dr лежит в плоскости, касательной к поверхности в точке M. Радиус-вектор нового положения точки M также удовлетворяет уравнению (31):(r + dr)
× (S × (r + dr)) = 1;опуская бесконечно малую величину второго порядка малости, получим
r
× (S × r) + dr × (S × r) + r × (S × dr) = 1.Первое слагаемое равно единице по формуле
(31), а второе и третье равны между собой благодаря симметричности S согласно соотношению (28). Отсюда получаемDr
× (S × r) = 0,т. е. вектор
b = S × r перпендикулярен любому dr, лежащему в касательной к поверхности в точке M плоскости, а значит, он перпендикулярен самой касательной плоскости, что и требовалось доказать.Главные оси тензора
Как известно из аналитической геометрии, существует такая система прямоугольных декартовых координат, в которой уравнение поверхности второго порядка (если отличны от нуля
S11, S22 и S33) принимает вид|
| (36) |
(случай конической поверхности не рассматриваем, считаем также, что
l1¢ , l2¢ и l3¢ имеют одинаковый знак). В этой системе координат недиагональные компоненты тензора равны нулю, и полуоси эллипсоида параллельны координатным осям, которые являются главными осями тензора. Матрица, соответствующая тензору S, в этой системе имеет диагональный вид (штрихи опускаем):
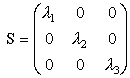
| (37) |
Величины
l1, l2 и l3 называются главными значениями тензора. Случаю, когда два из них равны друг другу, отвечает эллипсоид вращения, а если они все равны друг другу, тензорный эллипсоид превращается в сферу. В частности, единичному тензору соответствует сфера единичного радиуса:|
|
Из следующего рисунка видно, что на поверхности тензорного эллипсоида существуют такие точки, радиус-вектор которых направлен по нормали к поверхности, так что определяемый соотношением
(35) вектор b оказывается коллинеарным вектору r: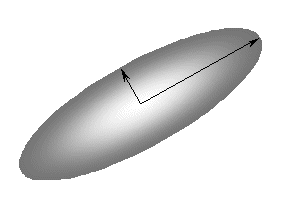
| b = l r, | (38) |
где
l – соответствующее главное значение тензора. Через эти точки проходят главные оси тензора. Действительно, в системе главных осей тензора
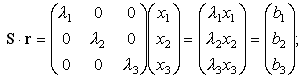
|
отсюда видно, что
b = l1r, когда r лежит на оси X1, и аналогично b = l2r, когда r лежит на оси X2 и b = l3r, когда r лежит на оси X3.Если левую и правую части соотношения (35) умножить на произвольный скаляр, то вместо радиус-вектора
r получим некоторый вектор a, и формулы (35) и (38) приведут к следующему соотношению:| S × a = la. | (39) |
Таким образом,
При умножении тензора на вектор, имеющий направление одной из главных осей тензора, направление вектора не изменяется, а его величина умножается на соответствующее главное значение тензора.
Равенство (39) справедливо в любой системе координат, если вектор
a параллелен одной из главных осей тензора. Это обстоятельство можно использовать для нахождения главных значений и главных направлений тензора.Распишем соотношение (39) в виде системы уравнений относительно неизвестных компонент вектора
a:| (S11 – l)a1 + S12a2 + S13a3 = 0; | |
| S21a1 + (S22 – l)a2 + S23a3 = 0; | (40) |
| S31a1 + S32a2 + (S33 – l)a3 = 0. |
Для того чтобы эта система имела нетривиальное (ненулевое) решение, необходимо, как известно из курса алгебры, чтобы определитель, составленный из ее коэффициентов, был равен нулю:
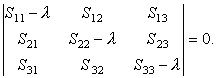
| (41) |
Соотношение (41) представляет собой кубическое уравнение относительно
l. Три его корня представляют собой главные значения тензора l1, l2 и l3. Подставив одно из найденных значений l в систему (40), из первых двух уравнений (третье является линейно зависимым от первых двух) находим соотношение между компонентами вектора a:|
| (42) |
Эти соотношения задают орт вектора
a и, следовательно, направление одной из главных осей тензора:
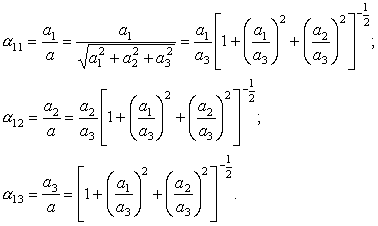
| (43) |
Оставшиеся два значения таким же образом позволяют найти направления двух других главных осей тензора
S.Скалярное умножение тензора и вектора с позиций алгебры является линейным преобразованием евклидова пространства, а вектор
a, удовлетворяющий соотношению (39), называется собственным вектором. В случае симметричного тензора линейное преобразование является симметрическим. Из курса алгебры известнаЛемма. Собственные векторы симметрического преобразования, относящиеся к различным собственным значениям, между собой ортогональны
Докажем ее применительно к симметричному тензору второй валентности. Перепишем соотношение (39) для двух различных собственных векторов
a1 и a2 (и соответственно собственных значений l1иl2):| b1 = S × a1 = l1a1; b2 = S × a2 = l2a2. |
Воспользуемся соотношением (28) для векторов
a1 и b2:| b2 × (S × a1) = a1 × (S × b2), |
или
|
l 2a2 × l1a1 = a1 × (S × l2a2) = l2a1 × (S × a2) = l2a1 × l2a2. |
После сокращения крайних частей этих равенств на
l2 получаем| (l1-l2)a2 × a1 = 0; | (44) |
поскольку
l1 ¹ l2, отсюда приходим к ортогональности собственных векторов a1 и a2. Аналогично доказывается ортогональность третьего собственного вектора a3 векторам a1 и a2.Согласно формуле (44) собственные векторы
a2 и a3 перпендикулярны вектору a1. Поэтому если направить ось X1 по вектору a1, проекции векторов a2 и a3 на эту ось будут равны нулю, и из системы (40) для a1 получим| (S11 – l) a1 = 0; S21 a1 = 0; S31 a1 = 0, |
откуда находим
| S21 = S12 = 0; S31 = S13 = 0, | (45) |
| (S11 – l) a1 = 0; | |
| (S22 – l) a2 + S23 a3 = 0; | (46) |
| S32 a2 + (S33 – l) a3 = 0. |
Для собственного вектора
a2 или a3 первое уравнение тождественно обращается в нуль, так что остаются два уравнения| (S22 – l) a2 + S23 a3 = 0; S32 a2 + (S33 – l) a3 = 0, |
или
|
|
откуда находим
|
| (47) |
при условии что
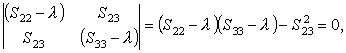
|
Эллипсоид вращения
Возможен случай, когда в выбранной системе координат
S22 = l, S33 = l и S23 = 0 (и остаются равенства S21 = S12 = 0; S31 = S13 = 0). При этом тензор S принимает диагональный вид
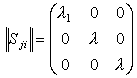
|
Это означает, что уравнение (41) имеет кратные корни:
l2 = l3 = l и l1 ¹ l. Поворот системы координат вокруг оси X1 оставляет вид тензора S неизменным: по формулам (8) и (I.24) получаем
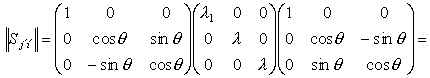 |
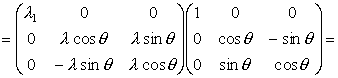 |
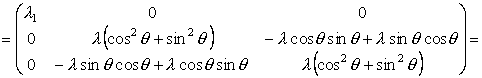 |
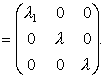 |
Следовательно, при двух кратных корнях (
l2 = l3 = l и l1¹ l) тензорный эллипсоид будет эллипсоидом вращения. При этом однозначно по формулам (43) определяется только один собственный вектор a1 и соответственно одна главная ось, совпадающая с осью симметрии эллипсоида. В качестве других главных осей можно взять две любые взаимно перпендикулярные оси, перпендикулярные оси симметрии эллипсоида.Если же все три корня уравнения (41) одинаковы (
l2 = l3 = l и l1 = l), тензорный эллипсоид вырождается в сферу, и в качестве главных осей можно взять три любые взаимно перпендикулярные оси.