II. Тензоры. 2.2. Тензорная алгебра

Сумма и разность тензоров

Определим сумму двух тензоров второй валентности T и G как тензор Q с компонентами

Если все компоненты тензора T умножить на один и тот же скаляр l, то в результате мы получим новый тензор с компонентами lT_ik…r. Если положить l=-1, от суммы двух тензоров нетрудно прийти к разности двух тензоров

Последние два утверждения очевидны при применении формулы (8) или (16).

Теорема. Всякий тензор валентности 2 может быть разложен, притом единственным способом, на сумму двух тензоров, из которых один будет симметричным, другой – антисимметричным.

Пусть дан тензор Q. Представим его в виде суммы симметричного S и антисимметричного A тензоров: Q = S + A. То же сделаем для сопряженных тензоров Q^* = S^* + A^*. Учитывая, что S^* = S и что A^*=-A, получим Q^*=S - A. Отсюда находим, что

Сумма тензоров есть тензор. Компоненты этих тензоров имеют вид

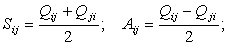(18)

Очевидно, первое выражение представляет компоненты симметричного тензора S, второе – антисимметричного тензора A, а компоненты исходного тензора могут быть записаны в виде

(19)

Сумма тензоров S и A дает исходный тензор Q, следовательно, теорема доказана.

Если компоненты тензора не меняются при перестановке любой пары индексов, такой тензор называют абсолютно симметричным. Если компоненты тензора меняют знак на обратный при перестановке любой пары индексов, такой тензор называют абсолютно антисимметричным.

Пусть даны тензор второй валентности T и вектор a. Под скалярным (внутренним) произведением тензора T и вектора a будем понимать новый вектор b = T× a, компоненты которого равны

здесь использованы соотношение (15) и свойства символа Кронекера. В соответствии с определением вектора по формулам (1.48) – (1.50) внутреннее произведение тензора и вектора является вектором.

Под скалярным (внутренним) произведением вектора a и тензора T будем понимать новый вектор c = a× T, компоненты которого равны

Аналогично скалярному произведению вектора и тензора определяется скалярное (внутреннее) произведение двух тензоров второй валентности T и G: Q=T× G. Компоненты этого тензора

Компоненты тензора G× T равны G_{i k}T_{k l}, т. е.

Как видим, внутреннее произведение тензоров некоммутативно.

Внешним произведением двух тензоров T и G второй валентности называется тензор Q четвертой валентности с компонентами

Так же определяется внешнее произведение тензоров произвольной валентности. У тензора – произведения сначала идут индексы первого сомножителя, затем – второго. Отсюда ясно, что и внешнее произведение тензоров некоммутативно. Валентность тензора, являющегося внешним произведением двух тензоров, равна сумме валентностей сомножителей. Так, например, внешнее произведение двух тензоров валентности 1 (векторов) a и b дает тензор C второй валентности с компонентами C_ik = a_i b_k.

Сверткой (свертыванием) тензора называется следующая операция: два индекса у всех компонент T_{i…qrs…uvw…y} тензора T принимаются одинаковыми, и по ним производится суммирование. Валентность получившегося тензора Q с компонентами

В случае, когда валентность тензора T равна 2, свертка дает тензор нулевой валентности, т. е. скаляр. Этот скаляр называется следом (или шпуром) тензора. Он равен сумме диагональных компонент тензора T:

Выясним, как преобразуются компоненты тензора валентности r при инверсии координатных осей, когда a _{j¢ i}=-d_{j¢ i}. В этом случае входящее в формулу (16) произведение

будет равно нулю, если хотя бы у одного символа Кронекера индексы имеют различные значения, или (–1)^r, если l¢ = i, k¢ = j,…,n¢ = m. Если r нечетно, все компоненты истинного тензора при инверсии координат меняют знак на обратный.

Псевдотензором валентности r в трехмерном пространстве называется совокупность 3^r величин, которые при поворотах ведут себя как компоненты обычного тензора, а при инверсии координат каждая компонента умножается на (–1) ^{r + 1}.

Если r нечетно, все компоненты псевдотензора при инверсии координат сохраняют знак. Результатом свертывания псевдотензора будет снова псевдотензор. Действительно, в результате свертки четность валентности сохраняется, а формулы преобразования инверсии отличаются множителем (–1)². Примерами псевдотензоров могут служить векторное произведение – псевдотензор первой валентности, любое произведение

псевдотензора P_ij…l и тензора T_mn…s. Чтобы убедиться в истинности последнего утверждения, достаточно рассмотреть следующую таблицу:

Примером псевдотензора служит также кососимметричный символ Кронекера e_ijk – единичный абсолютно антисимметричный псевдотензор третьей валентности. Рассмотрим этот вопрос подробнее.

При вращении системы координат компоненты кососимметричного символа Кронекера преобразуются как компоненты тензора. Действительно, рассмотрим соотношение

(27)

Введем следующие обозначения:

Здесь в качестве векторов u, v, w выступают орты штрихованной системы координат. Формула (27) с учетом соотношения (I.43) примет вид

Если индексы l¢ , m¢ и n¢ различны и получены путем циклической перестановки индексов 1¢ , 2¢  и 3¢ , справа мы получаем объем куба, построенного на трех ортах штрихованной системы координат, который равен единице. Аналогично если индексы l¢ , m¢  и n¢ различны и получены путем циклической перестановки индексов 1¢ , 3¢  и 2¢ , справа мы получаем объем того же куба, но со знаком “минус”, т. е. –1. В оставшихся случаях получается скалярное произведение взаимно перпендикулярных векторов, которое равно нулю.