

3.4. Ротор вектора. Формула Стокса
Ротор вектора
С оператором Гамильтона можно составить три простейшие конструкции:
| Ñj = gradj; |
| Ñ×A = divA; |
| Ñ´A = rotA. |
Последним соотношением определяется векторное поле, называемое ротором вектора
A.Рассмотрим произвольную точку М в векторном поле и произвольную малую площадку
S, ограниченную контуром L, на которой лежит точка M. Выберем произвольно направление обхода L и восстановим положительную нормаль n к площадке S в соответствии с п. 1.2. Ротором вектора a называется вектор (псевдовектор), проекция которого на направление вектора n равна пределу отношения
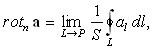
| (99) |
где обозначение
L ® P, подразумевает, что в процессе предельного перехода контур L стягивается в точку P. Ротор вектора в отечественной литературе еще называют вихрем вектора. В англоязычной литературе вместо rot a нередко используется обозначение curl a.|
Смысл его наиболее наглядно проявляется применительно к вектору скорости вращающегося твердого тела: v = w ´ r; рассмотрим круговой контур L малого радиуса R, плоскость которого перпендикулярна вектору w, а центр лежит в произвольной точке с радиус-вектором r0. В этом случае S = pR2; r = r0 + R. Выберем направление обхода контура так, чтобы соответствующее ему направление положительной нормали к S было направлено по вектору w. Тогда |  |
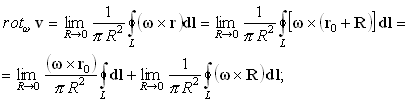
|
в первом интеграле правой части за знак интеграла вынесено не зависящее от координат контура
L векторное произведение, а интеграл вдоль замкнутого контура по вектору dl равен нулю. Во втором интеграле R ^ w; кроме того, векторное произведение в каждой точке контура L направлено по вектору dl, поэтому| (w´R)dl =wRdl; |
вынося за знак интеграла постоянный множитель
wR и учитывая, что оставшийся интеграл дает просто длину окружности 2pR, получим rot v = 2w, ротор линейной скорости точек вращающегося твердого тела равен удвоенной угловой скорости.Формула Стокса
|
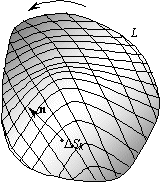
Рассмотрим произвольную кусочно-гладкую поверхность S в поле вектора a, ограниченную контуром L (не обязательно плоским). Произвольно зададим на контуре L направление обхода, которое определит направления положительных нормалей к поверхности S. Выберем малое число e; разобьем поверхность S на N столь малых элементов DSk, в сумме составляющих S, что для каждого из них, используя определение ротора (99), можно записать |
 |
Рассмотрим произвольную кусочно-гладкую поверхность
S в поле вектора a, ограниченную контуром L (не обязательно плоским). Произвольно зададим на контуре L направление обхода, которое определит направления положительных нормалей к поверхности S. Выберем малое число e; разобьем поверхность S на N столь малых элементов DSk, в сумме составляющих S, что для каждого из них, используя определение ротора (99), можно записать
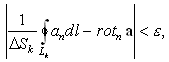
|
где
Lk – контур, ограничивающий DSk, а значение rota относится к некоторой точке элемента поверхности DSk. Направления обхода каждого из Lk соответствуют направлению положительной нормали к S на DSk согласно п. 1.2. Сложим эти выражения для всех элементов поверхности DSk, предварительно умножив их на DSk:
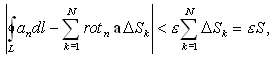
| (100) |
Здесь учтено, что линейные интегралы, взятые вдоль границ смежных элементов
DSk, взаимно сокращаются, так проходятся дважды в противоположных направлениях–один раз в контуре Lk, другой раз в смежном контуре Lk+1. вследствие противоположной ориентации смежных контуров. Нескомпенсированными останутся только линейные интегралы, взятые вдоль границ элементов DSk, совпадающих с участками контура L. Эти величины дадут в совокупности циркуляцию вектора a по всему контуру L. Входящая в левую сторону равенства интегральная сумма в пределе при N ® ¥ при max(DSk) ® 0 представляет собой поверхностный интеграл от rot a:
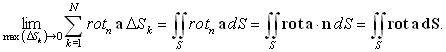
|
Так как
e мы можем взять сколь угодно малым, неравенство (100) приводит к соотношению
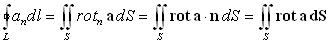
| (101) |
Таким образом, доказана следующая теорема:
Теорема Стокса. Циркуляция произвольного вектора по замкнутой кривой равна потоку ротора этого вектора через произвольную кусочно-гладкую поверхность, опирающуюся на данную кривую.
Мы по-прежнему предполагали, что однозначная функция
a(r) непрерывна и имеет непрерывные частные производные в некоторой области, в которой лежит поверхность S.
Ротор вектора в декартовых координатах
Выражение для проекции ротора на одну из координатных осей, например, ось
Z, в декартовой системе координат нетрудно определить, выбрав малую площадку S в виде прямоугольника со сторонами, параллельными другим координатным осям. Пусть координаты точки P – центра этой площадки–равны x0, y0, z0, а длины сторон соответственно Dx и Dy. Первоначально вычисляем линейные интегралы вектора a вдоль двух сторон, параллельных оси X. Координаты точек этих сторон: x, y0 ± Dy/2, z0. Направление обхода контура L в правой системе–против часовой стрелки. В этом случае вектором нормали к площадке будет служить орт e3. Поскольку| a(x, y0±Dy/2, z0.) = a(x, y0, z0) ± (¶a/¶y)Dy/2 + O(Dy)×Dy, |
где
O(Dy)–функция Dy, стремящаяся к нулю, сумма линейных интегралов по этим сторонам равна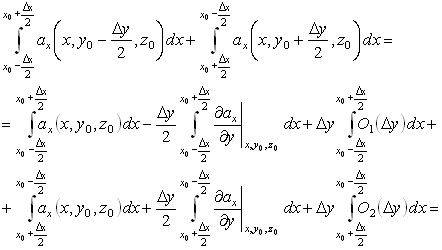
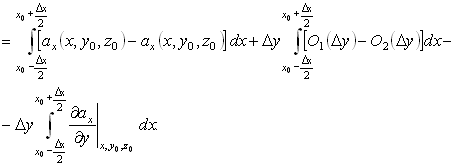
Первый интеграл обращается в нуль тождественно, второй, имея более высокий порядок малости, чем третий, после деления на
S = DxDy устремится к нулю при стягивании S в точку. Используя теорему о среднем, находим в первом приближении
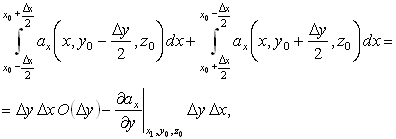
|
где производная ¶
ax/¶y взята в некоторой точке (x1, y0, z0) такой, что: x - Dx /2< x1<x + Dx/2. Аналогично для двух других сторон:
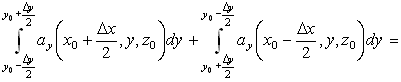
|
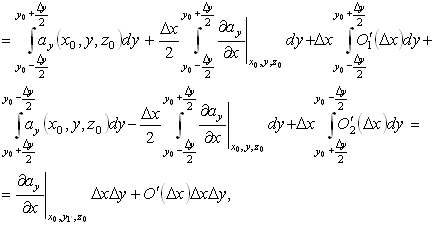
|
где производная
¶ay/¶x взята в некоторой точке (x0, y1ў, z0) такой, что y - Dy/2< y1ў<y + Dy/2. Итак, циркуляция вектора a вдоль выбранного контура L– прямоугольника со сторонами Dx и Dy равна
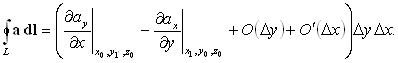
|
Подставляя в формулу (99), сокращая на
S и переходя к пределу S® P, получаем
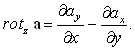
|
Аналогично находятся проекции ротора вектора
a на другие координатные оси. В итоге получим
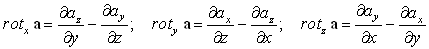
| (102) |
в полном соответствии с формулой
|
Ñ´a = rota. | (103) |
Некоторые следствия из теоремы Стокса
Если
a – потенциальный вектор, т. е. a = gradj, то, как мы знаем, линейный интеграл по всякому замкнутому контуру в односвязном пространстве равен нулю:
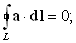
|
следовательно,
rot a = 0:| rot gradj = 0. | (104) |
Это ясно и непосредственно из выражений для ротора и градиента:
| rot gradj = eieijk¶2j /(¶xj¶xk)=0, |
поскольку единичный антисимметричный псевдотензор третьей валентности
eijk умножается на симметричный тензор второй валентности ¶2j/(¶xj¶xk), по индексам которого производится свертывание.Обратно, если в некоторой области пространства
rot a º 0, по формуле Стокса (101) для любого замкнутого контура этой области получаем
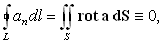
|
откуда следует потенциальность вектора
a в указанной области пространства, т. е. возможность представления вектора a вформе a = gradj. Таким образом, если|
e ijk¶aj/¶xkº0, i=1, 2, 3, |
то
|
aj = ¶j /¶xj, i=1, 2, 3, |
или, что то же,
|
a 1dx1+a2dx2+a3dx3 = dj ( x1, x2, x3), |
т. е. выражение в левой части является полным дифференциалом.
Необходимое и достаточное условие того,a чтобы был потенциальным вектором и чтобы выражение
a1dx1+a2dx2+a3dx3 |
было полным дифференциалом, состоит в тождественном равенстве ротора вектораa нулю.
Потенциальное поле называют также поэтому безвихревым.
Очевидно также, что
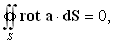
| (105) |
т. к. контур
L, по которому ведется интегрирование в левой части формулы Стокса (101), в этом случае стягивается в точку, и значение интеграла по такому контуру при ограниченной подынтегральной функции оказывается равным нулю. Обратившись к инвариантному определению дивергенции (89),
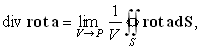
|
мы сразу получаем, что
|
div rot a º 0. | (106) |
Следовательно, векторное поле вихрей (роторов) любого вектора
a свободно от источников, т. е. соленоидально.Обратная теорема. Всякий соленоидальный вектор a может быть представлен как ротор некоторого другого вектора b: a = rot b.
Иными словами, если
div a º 0, то можно найти такой вектор b, что|
a = rot b. | (107) |
Для доказательства выберем такую систему декартовых координат, в которой
bz=0. Тогда выражение (107) в компонентах примет вид:|
ax = -¶by/¶z; ay = ¶bx/¶z; az = ¶bx/¶y - ¶by/¶x, | |
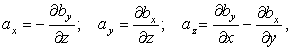
| (108) |
первые два уравнения можно переписать в виде
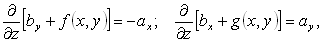
|
где
f(x,y) и g(x,y)–произвольные функции, не зависящие от z. Из этих соотношений находим
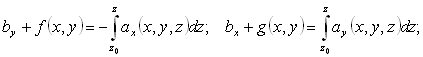
|
выразив отсюда
bx и by и подставив в третье из уравнений (108), получим
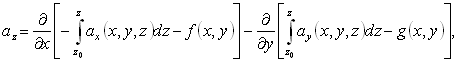
|
изменив порядок дифференцирования и интегрирования и объединив интегралы, получим
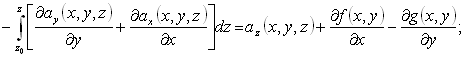
| (109) |
теперь учитывая, что
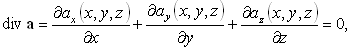
|
выразив первые две производные через последнюю, можем выполнить интегрирование:
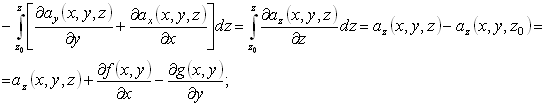
|
следовательно, уравнение (109) приводится к виду
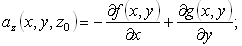
|
этому уравнению нетрудно удовлетворить, если положить
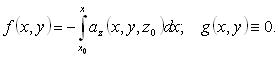
|
Итак, если в качестве
b выбрать вектор с компонентами
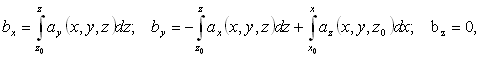
|
что, очевидно, возможно для любого векторного поля
a, равенство (107) a = rot b будет удовлетворено, что и требовалось доказать.