

3.3. Поток вектора через поверхность. Дивергенция вектора. Формула Гаусса-Остроградского. Источники
Пусть в некоторой области пространства имеется векторное поле
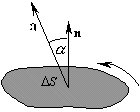
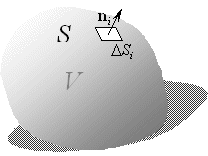
a(r). Выделим в этой области малую плоскую площадку DS. В пределах нее вектор a можно считать постоянным. Зададим произвольно направление обхода контура, являющегося границей площадки DS. Выберем в соответствии с п. 1.2 направление положительной нормали n к этой площадке.
|
Потоком вектора a через поверхностьDS называется скалярная величина, определяемая произведением:
| DN=a×n DS = a×DS = anDS. | (85) |
Рассмотрим теперь произвольную
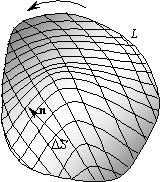
кусочно-гладкую поверхность S (Кусок поверхности S, заданный в параметрической форме x=x(u,v), y=y(u,v), z=z(u,v), где точка (u,v) пробегает некоторую область G плоскости u,v, называется гладким, если различные пары значений (u,v) дают разные точки S, частные производные функциий x(u,v), y(u,v), z(u,v) непрерывны, а ранг матрицы размером 2 x 3, составленной из этих производных, равен 2. Кусочно-гладкой называется поверхность, состоящая из конечного числа гладких кусков поверхности.). Одну из сторон поверхности назовем внешней и выберем соответствующим образом направление внешней нормали в каждой точке поверхности. Разобьем всю поверхность S на маленькие площадки DSi. Каждую такую площадку можно приближенно считать плоской, а вектор a в пределах площадки–постоянным. Суммарный поток через поверхность S складывается из элементарных потоков DNi, поэтому потоком вектора a через поверхность S называется предел интегральной суммы
|
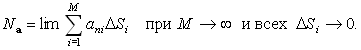
| (86) |
Этот предел называется
поверхностным интегралом и обозначается следующим образом:
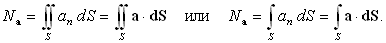
| (87) |
Использование для обозначения потока вектора значка двойного интеграла имеет тот смысл, что элементарная площадка
DSi может быть выражена через произведение двух приращений координат, при этом сумма окажется двойной. Например, в случае плоской поверхности, параллельной координатной плоскости XY, DSij = Dxi×Dyj; dS = dx×dy. Вектор a, поток которого определяется формулой (87), называют плотностью потока Na.Если поверхность
S замкнута, т. е. охватывает некоторый объем V со всех сторон (см. рис.), являясь его границей, то знак поверхностного интеграла (87) обычно снабжают кружком:
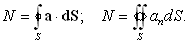
| (88) |
|
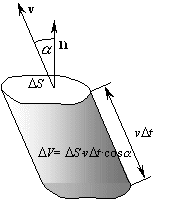
Название поток вектора заимствовано из гидродинамики. В случае поля скорости поток вектора
a(r) = v(r) определяет поток жидкости через поверхность S, то есть объем жидкости, протекающей через S в единицу времени (см. рис.: за время Dt весь изображенный объем, величина которого равна произведению площади основания DS на его высоту v×Dtcosa, и только этот объем пересечет площадку DS).
|
Рассмотрим произвольную точку
P векторного поля. Пусть S – произвольная замкнутая поверхность, окружающая точку P. И пусть V – объем, ограниченный этой поверхностью. Величина
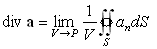
| (89) |
называется дивергенцией вектора
a в точке P (обозначение V ® P, подразумевает, что в процессе предельного перехода объем V стягивается в точку P). Дивергенция в переводе с латинского языка означает расходимость. Жидкость растекается из тех участков, где div v > 0. В этих участках расположены источники жидкости. По аналогии с гидродинамикой те точки поля, в которых diva> 0, называются точками истока, а точки, в которых div a < 0, называются точками стока. Векторные поля, у которых div a = 0 во всех точках, называются свободными от источников или соленоидальными (смысл последнего термина раскрывается ниже).Выражение для дивергенции в декартовой системе координат нетрудно определить, выбрав малый объем
V в виде прямоугольного параллелепипеда с гранями, перпендикулярными к координатным осям. Пусть координаты точки P–центра этого объема – равны x0, y0, z0, а длины ребер соответственно Dx, Dy, Dz. Первоначально вычисляем поток DNyz вектора a через две грани, перпендикулярные оси X. Координаты точек этих граней: x0 ± Dx/2, y, z. Поскольку|
a (x0 ± Dx/2, y, z) = a(x0, y, z) ± (¶ a/¶ x)Dx/2 + O(Dx)×Dx, | (90) |
где
O(Dx) – функция Dx, стремящаяся к нулю, суммарный поток из V через эти грани равен
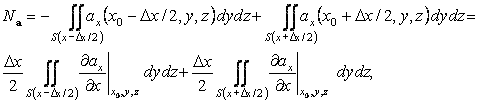
| (91) |
Используя теорему о среднем, находим в первом приближении
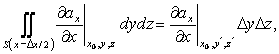
|
где производная
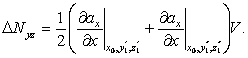
| (92) |
В этой формуле
величина V = DxDyDz. Аналогично можно рассчитать потоки через другие пары граней:
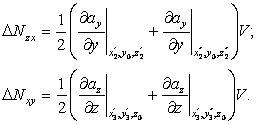
|
Подставляя в формулу (89)
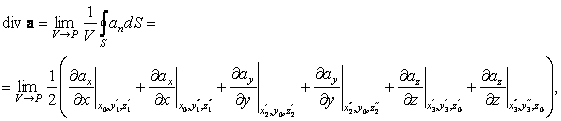
|
и переходя к пределу
V® P, получаем
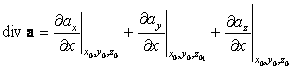
|
или просто
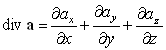
| (93) |
Рассмотрим область
V в поле вектора a, ограниченную поверхностью S. Выберем малое число e; разобьем объем V на N столь малых объемов DVk, в сумме составляющих V, что для каждого из них, используя определение дивергенции (89), можно записать
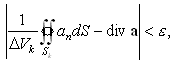
|
где
Sk – поверхность, ограничивающая DVk, а значение diva относится к некоторой точке объема DVk. Сложим эти выражения для всех элементарных объемов DVk, предварительно умножив их на DVk. При суммировании потоков потоки через общие поверхности соседних областей, очевидно, взаимно компенсируются. Действительно, потоки через общие поверхности отличаются знаками, так как для них внешние нормали имеют противоположные направления. Только потоки через участки внешней поверхности останутся нескомпенсированными. Поэтому при суммировании потоков результирующий поток будет представлять собой (в пределе при уменьшении элементарных объемов) поток вектора a через поверхность S. В результате получим
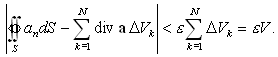
| (94) |
Входящая в левую сторону равенства интегральная сумма
в пределе при N ® ¥ при max(DVk) ® 0 дает объемный интеграл от дивергенции a:
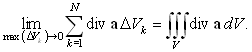
|
Последнее соотношение можно считать определением объемного интеграла от скалярной функции
f\(x, y, z) = div a. Вопросы существования такого предела рассматриваются в курсе математического анализа. Так как e мы можем взять сколь угодно малым, неравенство (94) неизбежно приводит к соотношению
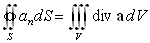
| (95) |
Соотношение (95) выражает собой теорему Гаусса–Остроградского:
поток вектораa через произвольную регулярную замкнутую поверхность равен интегралу от дивергенции этого вектора по объему, ограниченному данной поверхностью.
Соленоидальные поля
Векторные поля, у которых
diva = 0 во всех точках, называются свободными от источников или соленоидальными т.е. трубчатыми: в соленоидальном поле векторные линии могут быть замкнутыми, могут уходить на бесконечность, но не могут нигде ни начинаться, ни кончаться. Чтобы убедиться в этом, докажем основное свойство соленоидальных полей:Теорема 1. Поток соленоидального вектора через любое поперечное сечение векторной трубки имеет одну и ту же величину
Для доказательства применим формулу Гаусса
– Остроградского к объему V векторной трубки, ограниченному с торцов плоскими поверхностями S и S1:

|
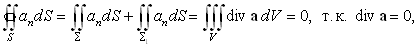
| (96) |
где учтено, что поток через боковую поверхность векторной трубки отсутствует (по определению векторной трубки на ней
an = 0). На поверхностях S и S1 направления внешней нормали различны относительно векторных линий, т. к. они направлены из объема V. Изменим поэтому направление нормали поверхности S на противоположное. Из формулы (96) тогда получим
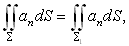
| (97) |
что и доказывает основное свойство соленоидальных полей. Отметим, что последнее соотношение справедливо и для несоленоидальных полей в тех областях пространства, в которых
div a = 0.Условимся при графическом изображении векторных полей проводить векторные линии так густо, чтобы число векторных линий, перпендикулярно пересекающих плоскую поверхность единичной площади, было пропорционально величине вектора. Другими словами, число изображаемых векторных линий, пересекающих произвольную площадку, должно быть пропорциональным потоку через эту площадку. Тогда из формулы (97) следует, что в тех областях пространства, где
div a = 0 (а для соленоидальных полей–везде), число векторных линий вдоль векторной трубки не меняется. Отсюда и следует, что в соленоидальном поле векторные линии нигде не могут ни начинаться, ни обрываться.Если на приведенном рисунке толщина векторной трубки достаточно мала, а поверхности
S и S1 перпендикулярны векторным линиям, формула (97) может быть переписана в виде|
a ×S = const, |
откуда следует, что величина вектора
a обратно пропорциональна площади поперечного сечения тонкой векторной трубки.Близким к доказанному является еще одно свойство соленоидальных полей, а также несоленоидальных полей
a(r) в тех областях пространства, в которых diva=0:Теорема 2. Если две поверхности S и S1 опираются на один и тот же контур L, то потоки соленоидального вектора a через эти две поверхности равны между собой, если поверхность S1 может быть непрерывной деформацией переведена в поверхность S и если после этой деформации направления нормалей к поверхностям S и S1 совпадут.
Для доказательства этого свойства достаточно применить формулу Гаусса–Остроградского к объему, ограниченному поверхностями
S и S1:

|
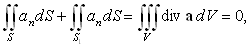
| (98) |
Изменив направление нормали у поверхности
S1 так, чтобы выполнялось условие, что после деформации S1 до совпадения с S направления нормалей к поверхностям S и S1 совпадут, получим соотношение вида (97) с S и S1 вместо S и S1, что и доказывает отмеченное свойство соленоидального поля.Доказанная теорема имеет аналогию с теоремой о независимости криволинейного интеграла потенциального вектора от пути интегрирования, потому что она может быть высказана еще в следующей форме:
Если векторa–соленоидальный, то поток этого вектора через любую поверхность S, натянутую на заданный контур L, не зависит от вида этой поверхности и зависит только от контура L.
Однако теорема о том, что криволинейный интеграл от потенциального вектора по замкнутому контуру равен нулю, справедлива только для случая односвязного пространства. Аналогично этому теорема 2 справедлива только для случая таких областей, в которых всякая поверхность типа сферической может быть стянута в точку без выхода за пределы области.