

3.2. Функции от векторного аргумента
Будем всегда предполагать, если только не оговорено обратное, что функции векторного аргумента непрерывны, т. е. Будем считать, что разности
j(r + Dr) - j(r) или a(r + Dr) - a(r) могут быть сделаны сколь угодно малыми при достаточно малом Dr.
Градиент. Потенциал векторного поля
Рассмотрим скалярное поле
j(r) = j( x1, x2, x3). Выберем некоторую точку M(r), проведем через нее произвольно ориентированную прямую и возьмем на ней соседнюю с M(r) точку M¢ (r + es), где e = MM¢ –малая величина, s–единичный вектор, направленный по прямой. При переходе от точки M(r) к точке M¢ (r+es) функция j(r) приобретает приращение Dj(r) = j(r + es) - j(r). Составим отношение Dj(r)/e, перейдем к пределу, устремив e к нулю, и назовем этот предел производной по направлению s в точке M:
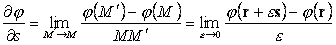
| (51) |
Знание производной ¶ j / ¶
s для любого направления позволяет вычислить во всех точках, соседних с точкой M, значение функции j с точностью до членов второго порядка малости.Для вычисления производной ¶ j / ¶
s введем декартову систему координат и примем во внимание, что|
si = cos(s,^xi), i = 1, 2, 3. | (52) |
Поэтому
j
(r + es) - j(r) = j(x1 + ecos(s,^x1), x2 + ecos(s,^x2), x3 + ecos(s,^x3)) - j(r).Эту разность можно рассматривать как сложную функцию аргумента
e. Разложим ее в ряд Тейлора, ограничившись членом, содержащим первую степень e:
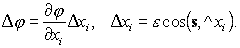
| (53) |
Формула (51) дает
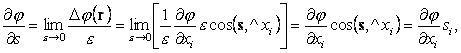
| (54) |
где, как и выше, используется правило Эйнштейна. Последняя формула имеет вид скалярного произведения (
a×b = aibi) и может быть переписана в виде
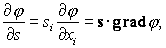
| (55) |
этим соотношением и определяется градиент скалярной функции
j:
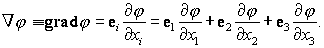
| (56) |
Производную ¶ j / ¶
xi можно рассматривать как действие некоторого оператора ¶ / ¶ xi на функцию j (r). Аналогично можно определить векторный оператор
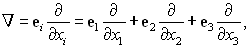
| (57) |
который, действуя на скалярную функцию, дает ее градиент. Знак Ñ читается как “набла” и называется оператором Гамильтона.
Соотношение (54) может быть получено также следующим образом. Рассмотрим дифференциал функции
j(x1,x2,x3):
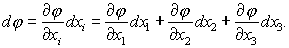
|
И в этом выражении просматривается скалярное произведение двух векторов, которое можно представить в виде
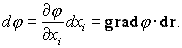
| (58) |
Разделив левую и правую части на
ds, придем к формуле (54). Таким образом, производная скаляра по направлению равна проекции вектора градиента на это направление. Направление градиента является направлением наиболее быстрого возрастания скалярной функции j.Обратимся к соотношению (58). Допустим, что точка
M¢ принадлежит той же поверхности уровня, на которой лежит точка M. В этом случае|
d j = 0; grad j × dr = 0. | (59) |
Следовательно, вектор
dr, лежащий на поверхности уровня функции j (x1, x2, x3), перпендикулярен градиенту этой функции. А поскольку на этой поверхности он может принимать любое направление, лежащее в касательной плоскости, отсюда следует, чтоградиент функцииj (x1, x2, x3), перпендикулярен поверхности уровня этой функции.
И если единичный вектор нормали к поверхности уровня в некоторой точке обозначить посредством
n, а производную по направлению n–посредством ¶j/¶n, очевидно, будем иметь
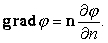
| (60) |
Далее находим
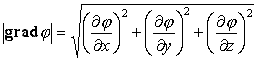
| (61) |
Очевидно,
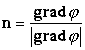
| (62) |
Вернемся к формуле (58). Если мы найдем такой вектор
a, что для произвольного dr имеет место равенство|
d j = a × dr | (63) |
то можно утверждать, что
a = gradj.Нетрудно убедиться, что имеют место равенства
|
grad (j + y) = gradj + grady; | (64) |
|
grad(j y) = y gradj + jgrady; | (65) |
|
grad F(j) = F¢gradj; | (66) |
Вектор, являющийся градиентом некоторого скаляра j , называется потенциальнымвектором, а поле такого вектора – потенциальным полем. Функция j(r) называется потенциалом векторного поля.
Несмотря на свой простой характер, формула (6
4) имеет важное значение, поскольку на ней основано сложение потенциальных векторных полей. Если a = grad j и b = grad y, то c = a + b является градиентом функции j + y.
Линейный интеграл
Потенциальные векторные поля обладают особыми свойствами, связанными с понятием линейного интеграла вдоль некоторой кривой.
Пусть нам задано поле вектора a(r). Возьмем какую-нибудь кривую L, соединяющую точки M0(r0) и M(r). Считаем ее ориентированной, т. е. на ней определено положительное направление от точки M0 к точке M. Разобьем ее мысленно на малые элементы, которые заменим хордами Dl, и составим сумму скалярных произведений a(r) × Dl, включающую все упомянутые хорды.
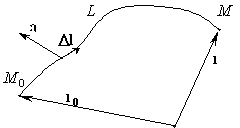
|
Предел этой суммы при
Dl ® 0
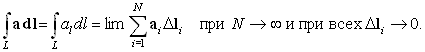
| (67) |
называется линейным (или криволинейным) интегралом вектора
a вдоль кривой L. В общем случае поля, которое нет оснований считать потенциальным, значение этого интеграла зависит от длины и формы кривой (к примеру, работа по передвижению тумбы для награждения победителей среди конькобежцев зависит от того, по льду или снегу, напрямую или в обход будут тащить эту тумбу). Поэтому в отличие от обыкновенного определенного интеграла у линейного интеграла указывают не пределы интегрирования (такого понятия у линейного интеграла нет), а область интегрирования–саму кривую L. При общеупотребительной краткой записи линейного интеграла
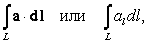
|
подразумевается, что кривая
L каким-либо образом описана. Линейный интеграл вдоль замкнутой кривой называется циркуляцией вектора по этой кривой и обозначается следующим образом:|
подразумевается, что кривая L каким-либо образом описана. Линейный интеграл вдоль замкнутой кривой называется циркуляцией вектора по этой кривой и обозначается следующим образом: |
 |
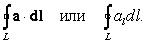
|
Для потенциального векторного поля имеет место следующая весьма важная теорема.
Еслиj – однозначная функция, то значение линейного интеграла grad j не зависит от пути интегрирования, а определяется только положением начальной и конечной точек интегрирования.
Действительно,
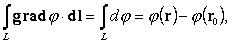
| (68) |
т. к он представляет собой предел суммы приращений потенциала
j:|
Dj 12 = j2 - j1; |
|
Dj 23 = j3 - j2; |
|
. . . . . . . . . . . . . . |
|
Dj n–1 n = jn - jn–1; |
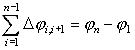
|
Отсюда следует, в частности, что циркуляция потенциального вектора вдоль замкнутого контура равна нулю:
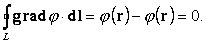
|
Обратная теорема:
Если линейный интеграл вектораa вдоль всякой замкнутой кривой равен нулю, вектор a является потенциальным, т. е. представим градиентом некоторого скаляра.
Доказательство.
|
В первую очередь заметим, что в этом случае интеграл, взятый по некоторому пути L от некоторой точки M0(r0) до другой точки M(r), будет таким же, как и взятый по любому иному пути L’ от точки M0(r0) до точки M(r). Действительно, из этих двух кривых L и L’ можно образовать замкнутый контур и вычислить вдоль него линейный интеграл, в котором если кривая L проходится от точки M0(r0) до точки M(r) то кривая L’ проходится от точки M(r) до точки M0(r0): |
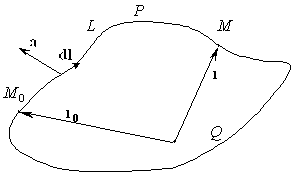 |
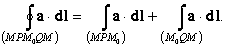
|
Интеграл вдоль кривой
L¢ от точки M0(r0) до точки M(r) будет отличаться от интеграла вдоль этой же кривой от точки M(r) до точки M0(r0) только знаком. Это ясно из того, что при перемене направления в сумму бесконечного числа бесконечно малых слагаемых (в интеграл) будут входить (в обратном порядке) величины a×dl, в которых вектор dl имеет просто противоположное направление:
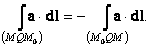
| (69) |
Таким образом,
![]()
последнее означает, что
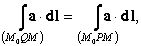
|
т. е. значение интеграла не зависит от кривой и определяется только положениями конечных точек. Следовательно, при фиксированной точке
M0 он является функцией r. Обозначим эту функцию как j(r):
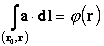
| (70) |
Взяв элементарные приращения обеих частей этого равенства при бесконечно малом перемещении
dl, получим|
a × dl = dj (r). | (71) |
Сравнивая последнее выражение с формулой (58), в силу произвольности направления вектора
dl приходим к равенству|
a = grad j, | (72) |
что и требовалось доказать.
Теорема о том, что значение линейного интеграла
gradj не зависит от пути интегрирования, доказывается в предположении, что j–однозначная функция. Одного примера достаточно для того, чтобы убедиться: если требование однозначности функции j не выполняется, значение линейного интеграла gradj неоднозначно. Пусть j = arctg(y/x). Рассмотрим линейный интеграл gradj по дуге радиуса r с центром в начале координат, лежащей в плоскости XY. На ней x2 + y2 = r2. Касательный к дуге вектор s лежит на прямой, тангенс угла наклона которой равен производной dy/dx:
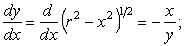
|
при проходе дуги в направлении против часовой стрелки компоненты вектора
s будут равны (–y/r, x/r, 0). Градиент функции j имеет компоненты

|
их скалярное произведение равно
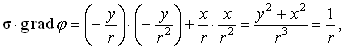
|
поэтому линейный интеграл
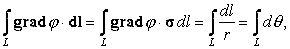
|
где угол
q монотонно растет вдоль дуги, достигая значения 2 p при замыкании дуги, когда начальная и конечная точки совпадают.Следует отметить, что при приближении к оси
Z значение функции j (r) становится неопределенным. Поэтому ее следует рассматривать в области, не содержащей ось Z. Для этого окружим ее цилиндром малого радиуса бесконечной длины и будем рассматривать функцию j (r) вне объема этого цилиндра. Но получающаяся при этом область не будет односвязной:Односвязным называется такое пространство, в котором любая замкнутая линия может быть стянута в точку непрерывным образом, не задевая границ области.
В нашем случае этого сделать нельзя, т. к. контур, охватывающий ось
Z, не может быть стянут в точку. Таким образом,в случае многосвязного пространства потенциал может быть многозначным, и потому линейный интеграл его градиента может зависеть от пути интегрирования. В частности, интеграл по замкнутому контуру может оказаться не равным нулю.
Примеры применения градиента в физике
Если в газе, жидкости или изотропном твердом теле температура неоднородна, в нем возникают тепловые потоки с плотностью
|
q = -l grad T, |
где
l – коэффициент пропорциональности, зависящий от свойств вещества и называемый теплопроводностью.В гидромеханике рассматриваются, наряду с вихревыми, потенциальные течения, в которых поле скоростей жидкости потенциально, так что
|
v = grad j. |
Электрическое поле неподвижных заряженных частиц потенциально:
|
E = -grad j; |
в частности, потенциал поля точечного заряда
e равен ke/R, где R – расстояние от него, а k – коэффициент, зависящий от системы единиц. Вычисление градиента такого потенциала дает
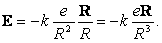
|
Производная вектора по направлению
Градиент скалярного поля
j(r) играет по сути ту же роль, что и производная скалярной функции одного аргумента dj(t)/dt, но является уже вектором, т. е. валентность тензора при дифференцировании по координатам повысилась на единицу. Если ввести аналогичную величину для векторного поля, его валентность также увеличится на единицу, что даст тензор второй валентности с компонентами ¶ai/¶xj. Такие величины рассматриваются в тензорном анализе. Чтобы не выходить за рамки векторного анализа, ограничимся пока рассмотрением производной вектора по направлению.Рассмотрим некоторое векторное поле
a(r) = a(x1, x2, x3). Снова выберем некоторую точку M(r), проведем через нее произвольно ориентированную прямую и возьмем на ней соседнюю с M(r) точку M¢ (r + es), где e = MM¢ –как и ранее, малая величина, а s–единичный вектор, направленный по прямой. При переходе от точки M(r) к точке M¢ (r + es) функция a(r) приобретает приращение Da(r) = a(r + es) - a(r). Составим отношение Da(r)/e, перейдем к пределу, устремив e к нулю, и назовем этот предел (если он существует) производной вектора a по направлению s в точке M:
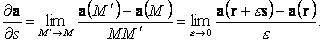
| (73) |
Как и в случае формулы (54), получаем
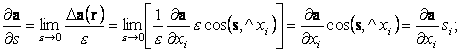
| (74) |
можно ввести дифференциальный оператор
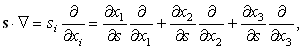
| (75) |
действие которого на векторное поле
a(r) дает правую часть формулы (74):
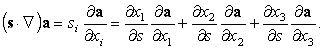
| (76) |
Аналогично оператору (75) можно ввести оператор
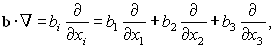
| (77) |
результатом действия которого на векторное поле
a(r) будет вектор
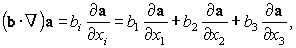
| (78) |
направление которого, очевидно, лишь в некоторых случаях может совпасть с направлением вектора
a(r). Он называется градиентом вектора a(r) по вектору b. Если обозначить этот вектор через c, то его i-ая компонента имеет вид
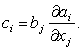
| (79) |
В векторе
c = (bÑ )a нетрудно увидеть свертку вектора b с тензором второй валентности ¶ ai/¶ xj.Пример применения градиента по вектору
При движении жидкости как сплошной среды в ней имеется некоторое векторное поле скоростей
v(r, t), а также скалярные поля давления p(r, t), и температуры T(r, t). Обозначим посредством f(r, t) любую из компонент скорости или давление или температуру. Можно изучать изменение данной величины со временем в фиксированной точке пространства, и скорость ее изменения определится частной (локальной) производной по времени ¶f /¶ t:
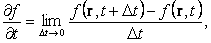
| (80) |
при вычислении которой радиус-вектор
r рассматривается как постоянный.| С другой стороны, можно изучать изменение со временем конкретной “жидкой частицы”–некоторой малой части одной из трубок тока выделенного объема. Чтобы охарактеризовать это изменение, нужно сравнить значения f(r, t) в точке M(r), в которой “жидкая частица” находилась в момент t, и в точке M¢ (r + Dr), в которой она окажется в момент t + Dt. Предел отношения разности этих значений к Dt |  |
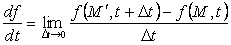
| (81) |
называется полной, или субстанциональной производной
f(r, t) по t. При вычислении этой производной нужно координаты “жидкой частицы” считать функциями времени, причем
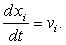
|
Рассматривая
f(r, t) как сложную функцию от t, получим
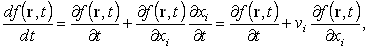
|
или
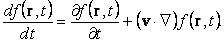
| (82) |
Второе слагаемое правой части называют конвективным членом, так как он появляется только при движении сплошной среды и связан с обусловленным этим движением конвективным переносом “жидких частиц”.
Если понимать под
f(r, t) любую из компонент скорости жидкости, формула (82) примет вид
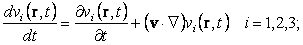
| (83) |
умножая каждое из этих трех уравнений на соответствующий орт и складывая, получаем
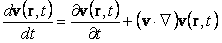
| (84) |
Эта формула, очевидно, описывает ускорение
“жидкой частицы”.