I. Векторы. 1.6. Векторная алгебра с использованием компонент векторов

Правило Эйнштейна. Символ Кронекера

Запись суммы составляющих вектора a

a = a1 e1 + a2 e2 + a3 e3

с использованием знака суммы

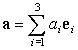
зачастую заметного выигрыша в лаконичности не дает. Эйнштейном предложено правило, позволяющее значительно сократить запись формул, содержащих суммирование компонент векторов и тензоров.

Суммирование всегда производится по тем и только по тем значкам, которые дважды появляются под знаком суммы. Поэтому можно без ущерба для ясности отбросить знак суммы: если член некоторого выражения содержит какой-нибудь индекс дважды, то по этому значку должно быть произведено суммирование, если только специально не оговорено противное.

Иными словами, при суммировании компонент векторов и тензоров знак суммы не пишется; суммирование обнаруживается по наличию в слагаемых выражения индексов, встречающихся дважды.

В соответствии с этим правилом мы имеем

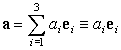(34)

Скалярное произведение двух векторов a и b тогда запишется в виде

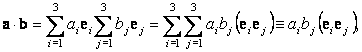(35)

Очень важный момент: нельзя в разных суммах использовать один и тот же символ, по которому ведется суммирование, так называемый немой индекс. Это очевидно из следующих соотношений, которые легко могут быть обобщены на произвольное число сомножителей в суммах:

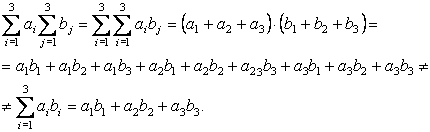
Поэтому наличие одинакового индекса более чем у двух сомножителей в одночлене свидетельствует или об ошибке, или о том исключении из правила Эйнштейна (специально оговорено противное), когда суммирование по этим индексам не ведется

Скалярное произведение (ei ej), входящее в сумму (35), может быть равно только нулю при i ¹ j или только единице при i = j: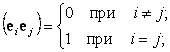

(36)

для сокращенного обозначения этих соотношений удобно использовать так называемый символ Кронекера, определяемый следующим образом:

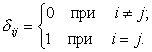(37)

Символ Кронекера может быть представлен также единичной матрицей (первый индекс указывает номер строки, второй – номер столбца):

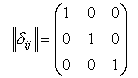(38)

С учетом соотношений (36) соотношения (35) преобразуются следующим образом: рассмотрим сначала внутреннюю сумму; при этом индекс i остается фиксированным, он изменяется только во внешней сумме. Поскольку при i ¹ j (ei ej) = 0, в сумме останутся только такие слагаемые, у которых i = j. При этом (ei ej) = 1, так что получаем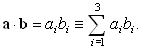

(39)

В дальнейшем знак суммы опускаем и всегда используем правило Эйнштейна.

Кососимметричный символ Кронекера

Введем символ eijk, означающий упорядоченную совокупность 32 = 27 чисел, каждое из которых равно 0, 1 или – 1. Каждому значению k = 1,2,3 соответствует квадратная матрица значений символа eijk: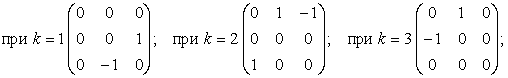

(40)

для наглядности сопоставим им матрицу индексов ijk: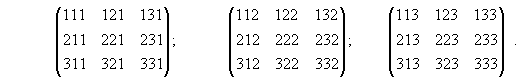

 Как видим, eijk = 1, если i = 1; j = 2; k = 3 или значения индексов такие, которые получаются циклической перестановкой этих значений, т. е. всего три числа из 27 равны единице (e123 = 1, e312 = 1, e231 = 1); при нециклической перестановке значений индексов (при перестановке значений любой пары индексов) знак eijk меняется на противоположный; таким образом, e132 = – 1, e321 = – 1, e213 = – 1; если встречаются два или три одинаковых значения индексов (все, кроме перечисленных), eijk = 0. Другими словами, значения символа eijk можно определить так: они равны нулю при совпадении значений хотя бы двух индексов; они равны + 1 или – 1 в зависимости от того, каким – четным или нечетным числом перестановок может быть получена последовательность i j k из последовательности 1 2 3. Эта совокупность чисел называется кососимметричным символом Кронекера (о другом названии – несколько позже).

Из определений символа Кронекера и кососимметричного символа Кронекера следуют тождества

eijk dij = eijk djk = eijk dki = 0. (41)

Действительно, если значения индексов символа Кронекера совпадают, совпадающими оказываются значения индексов кососимметричного символа Кронекера, который в этом случае равен нулю. В противном случае равен нулю символ Кронекера dki, так что в любом случае их произведение равно нулю. Таким образом, сумма (41) состоит только из нулевых слагаемых и равна нулю.

С помощью кососимметричного символа Кронекера можно компактно записать векторное произведение через его компоненты:

a ´ b = ei eijk aj bk. (42)

Действительно, в этой тройной сумме (по i, j и k) отличными от нуля будут только слагаемые

 

e1 a2 b3

при i = 1,

j = 2,

k = 3;

–

e1 a3 b2

при i = 1,

j = 3,

k = 2.

–

e2 a1 b3

при i = 2,

j = 1,

k = 3;

–

e2 a3 b1

при i = 2,

j = 3,

k = 1;
 

e3 a1 b2

при i = 3,

j = 1,

k = 2;

–

e3 a2 b1

при i = 3,

j = 2,

k = 1.

Смешанное произведение, с учетом соотношений (34) и (42), запишется через компоненты в виде

c × (a ´ b) = eijk ci aj bk. (43)

Имеет место важное соотношение:

eijk emnk = dim djn – din djm (44)

Докажем его. Распишем сумму по k левой части равенства:

eijk emnk = eij1 emn1 + eij2 emn2 + eij3 emn3 = dim djn – din djm.

Очевидно, что все слагаемые и левой и правой частей обратятся в нуль, если i = j или m = n. При этом формула (44) верна.

Если i¹ j и одновременно m ¹ n, то eijkemnk ¹ 0, только если i = m и j = n или i = n и j= m. Действительно, в первом слагаемом ни один из них не должен быть равным 1, чтобы оно не было равным нулю, во втором – 2, в третьем – 3. Такое возможно только если i = m или i = n и соответственно j = n или j = m. В противном случае и левая, и правая части обращаются в нуль, так что формула (44) верна.

Рассмотрим случаи, когда i = m и j= n или i = n и j = m. В первом варианте имеем

(emn1)2 + (emn2)2 + (emn3)2 = 1 – (dmn)2,

причем m¹ n. Правая часть равна единице, а в левой только одно слагаемое и обязательно одно равно единице. Если же i = n и  j= m, аналогично, с учетом того что enmk = -emnk, получаем

–(enm1)2 – (enm2)2 – (enm3)2 = (dnm)2 – 1,

причем опять же m¹ n. Правая часть равна минус единице, а в левой снова одно слагаемое и только одно равно минус единице.

Тем самым, поскольку перебраны всевозможные варианты соотношений между индексами, формула (44) доказана.

Формула (44) имеет большую важность при раскрытии двойного векторного произведения. Докажем с ее помощью формулу “бац минус цаб”. При записи внимательно следим за индексами, чтобы не допустить появления более двух одинаковых индексов в каждом из слагаемых:

B ´ c = ek ekmn bm cn;

a ´ (b ´ c) = ei eijk aj (b ´ c)k = ei eijk aj ekmn bm cn =

= ei aj bm cn eijk ekmn = ei aj bm cn eijk emnk =

= ei aj bm cn (dim djn – din djm) = ei aj bm cn dim djn – ei aj bm cn din djm =

= ei aj bi cj – ei aj bj ci = (ei bi) (aj cj) – (ei ci) (aj bj) = b (aЧc) – c (aЧb).

Здесь использованы тождества

ekmn = emnk; bm dim = bi; cn djn = cj; (ei bi) = b; (aj bj) = (aЧb).

Формулы преобразования компонент вектора

С использованием правила Эйнштейна весьма компактно записываются формулы преобразования компонент вектора при переходе от одной системы координат к другой, повернутой относительно первой произвольным образом. Формулы (17) перепишем сначала в виде

x1¢ = a1¢ 1 x1 + a1¢ 2 x2 + a1¢ 3 x3;

x2¢ = a2¢ 1 x1 + a2¢ 2 x2 + a2¢ 3 x3;

x3¢ = a3¢ 1 x1 + a3¢ 2 x2 + a3¢ 3 x3;

их можно представить следующим образом:

xj¢ = a j¢ ixi , где a j¢ i = (ej¢ ei) (45)

аналогично обратные соотношения (18) принимают вид

x1 = a1¢ 1 x1¢ + a2¢ 1 x2¢ + a3¢ 1 x3¢ ;

x2 = a1¢ 2 x1¢ + a2¢ 2 x2¢ + a3¢ 2 x3¢ ;

x3 = a1¢ 3 x1¢ + a2¢ 3 x2¢ + a3¢ 3 x3¢ ,

или

xi = aj¢ i xj¢ . (46)

Эти последние две формулы различаются лишь тем, что в первом случае суммирование ведется по второму индексу, а во втором – по первому.

В соотношениях (19) и (20) тоже сначала заменим ak, bk и gk на a j¢ i:

a1¢ 1 a1¢ 1 + a2¢ 1 a2¢ 1 + a3¢ 1 a3¢ 1 = 1;

a1¢ 2 a1¢ 2 + a2¢ 2 a2¢ 2 + a3¢ 2 a3¢ 2 = 1;

a1¢ 3 a1¢ 3 + a2¢ 3 a2¢ 3 + a3¢ 3 a3¢ 3 = 1;

a2¢ 1 a3¢ 1 + a2¢ 2 a3¢ 2 + a2¢ 3 a3¢ 3 = 0;

a1¢ 1 a2¢ 1 + a1¢ 2 a2¢ 2 + a1¢ 3 a2¢ 3 = 0;

a3¢ 1 a1¢ 1 + a3¢ 2 a1¢ 2 + a3¢ 3 a1¢ 3 = 0.

Все эти шесть соотношений могут быть представлены в форме

am¢ i an¢ i = dm¢ n¢ , где m¢ = 1, 2, 3; n¢ = 1, 2, 3. (47)

Это ясно и из следующего рассмотрения: a m¢ ian¢ i = (em¢  ei)(en¢  ei), а (em¢  ei) можно рассматривать как проекции векторов em¢ на оси xi исходной системы координат и (en¢ ei) как проекции en¢ на те же оси xi. Тогда, следуя формуле (39), выражающей скалярное произведение векторов a и b, где также суммируются их проекции на координатные оси xi: ab = aibi = (a ei) (b ei), можем записатьa m¢ i an¢ i = em en¢ = dm¢ n¢ .

Их можно получить и непосредственно из формул (45) и (46). Подставим в формулу (46) xj¢ из формулы (45), предварительно поменяв в той немой индекс на k: xj¢ = a j¢ k xk.

xi = aj¢ i xj¢ = aj¢ i a j¢ k xk. = (aj¢ ia j¢ k) xk..

В силу независимости компонент радиус-вектора выражение в скобках должно быть отличным от нуля и равняться единице только если j = k.Таким образом приходим к формуле (47).

По формулам (45) и (46) преобразуются также компоненты любого вектора, а не только радиус-вектора, проведенного из начала координат:

aj¢ = a j¢ iai(48)
ai = aj¢ i aj¢ , (49)

где

a j¢ i = (ej¢ ei) (50)

Алгебраическое определение векторов

Если совокупность величин a1, a2, a3 при переходе от одной прямолинейной прямоугольной системы координат к другой преобразуется по формулам (48) – (50), совокупность этих трех величин a1, a2, a3 определяет новую величину a, называемую вектором.

Такое определение, не требующее геометрической интерпретации, имеет еще одно преимущество: оно позволяет аналогичным образом определить векторы в n-мерном пространстве, в частности, в 4-мерном пространстве – времени.