Глава I. Преобразование составляющих вектора

I. Векторы. 1.3. Преобразование составляющих вектора при переходе от одной системы координат к другой

Пусть имеется два ортогональных базиса: e₁, e₂, e₃ и e_1¢, e_2¢, e_3¢. Вектор a можно согласно соотношению (5) представить в виде

a = a₁ + a₂ + a₃,

где a₁, a₂, a₃ коллинеарны ортам первого базиса:

a₁ = a₁e₁, a₂ = a₂e₂, a₃ = a₃e₃.

Рассмотрим проекцию этого вектора на направление некоторого вектора u:

a_u = acos (a,^{^}u)=a₁ a + a₂ b + a₃ g,

(15)

где для краткости введены обозначения

a = cos(e₁,^{^}u), b = cos(e₂,^{^}u), g = cos(e₃,^{^}u).

Вектор a можно также согласно тому же соотношению (5) представить в виде

a = a_1¢ + a_2¢ + a_3¢,

где a_1¢, a_2¢, a_3¢ коллинеарны ортам второго базиса:

a_1¢ = a_1¢e_1¢, a_2¢ = a_2¢e_2¢, a_3¢ = a_3¢e_3¢.

Как выражаются новые компоненты a_1¢, a_2¢, a_3¢ вектора a через старые a₁, a₂, a₃ ? Ответ дается формулой (15). Положим в ней последовательно u = e_1¢, e_2¢, e_3¢:

a_1¢ = a₁a₁ + b₁a₂ + g₁a₃, где a₁ = (e₁e_1¢) , b₁ = (e₂e_1¢) , g1 = (e₃e_1¢);
a_2¢ = a₂a₁ + b₂a₂ + g₂a₃, где a₂ = (e₁e_2¢) , b₂ = (e₂e_2¢) , g₂ = (e₃e_2¢)	(16)
a_3¢ = a₃a₁ + b₃a₂ + g₃a₃ , где a₃ = (e₁e_3¢) , b₃ = (e₂e_3¢) , g₃ = (e₃e_3¢).

Скалярное произведение единичных векторов равно косинусу угла между ними. В частности, если вектором a является радиус-вектор r, проведенный из начала координат,

a₁ = x₁; a₂ = x₂; a₃ = x₃; a_1¢ = x_1¢; a_2¢ = x_2¢; a_3¢ = x_3¢ ,

так что

x_1¢ = a₁x₁ + b₁x₂ + g₁x₃;
x_2¢ = a₂x₁ + b₂x₂ + g₂x₃	(17)

и обратно

x₁ = a₁x_1¢ + a₂x_2¢ + a₃x_3¢;
x₂ = b₁ x_1¢ + b₂ x_2¢ + b₃ x_3¢;	(18)
x₃ = g₁ x_1¢ + g₂ x_2¢ + g₃ x_3¢.

В этих соотношениях

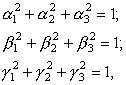(19)

т. е. не все эти коэффициенты независимы. Если в последнем из соотношений (16) положить a = e_2¢ , то a_3¢ = 0, a₁ = e_2¢ e₁ = a₂; a₂ = e_2¢ e₂ = b₂; a₃ = e_2¢ e₃ = g₂; аналогично поступаем с предыдущим уравнением в (16), где полагаем a = e_1¢, и с первым, в котором полагаем a = e_3¢. Это дает нам три соотношения

a₁a₃ + a₂b₃ + a₃g₃ = a₂a₃ + b₂b₃ + g₂g₃ = 0;
a₁a₂ + a₂b₂ + a₃g₂ = a₁a₂ + b₁b₂ + g₁g₂ = 0	(20)
a₁a₁ + a₂b₁ + a₃g₁ = a₃a₁ + b₃b₁ + g₃g₁ = 0.

Рассмотрим частный случай, когда один из ортов первого базиса совпадает с соответствующим ортом второго базиса, например, e_3¢ = e₃. Тогда

g₁ = (e₃e_1¢) =0; g₂ = (e₃e_2¢) =0; g₃ = (e₃e_3¢ )=1; a₃ = (e₁e_3¢ )=0; b₃ = (e₂e_3¢)=0.	(21)
	(22)

Если обе координатные системы правые, так что имеем поворот одной координатной системы относительно другой вокруг направления орта e₃ на угол q без отражения.

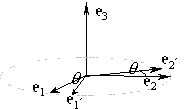
В этом случае

a₁ = (e₁e_1¢) ; b₁ = (e₂e_1¢) ; a₂ = (e₁e_2¢) ; b₂ = (e₂e_2¢) ;

из рисунка видно, что a₁ = (e₁e_1¢ ) = (e₂e_2¢ ) = b₂; соотношения (22) принимают вид

из последнего соотношения получаем

a₂ = – b₁.

В итоге имеем соотношения

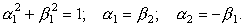(23)

Положим a₁ = b₂ = cosq; b₁ = – a₂ = sinq; тогда из соотношений (16) получаем

a_1¢ = a₁ a₁ + a₂ b₁ ; a_1¢ = a₁cosq + a₂sinq;
a_2¢ = a₁ a₂ + a₂ b₂ ; a_2¢ = – a₁sinq + a₂cosq,	(24)
a_3¢ = a₃; a_3¢ = a₃;