

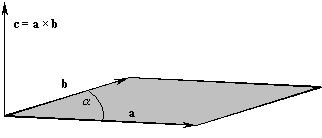
I. Векторы. 1.2. Вектор площади. Псевдовекторы
Векторным или внешним произведением двух векторовa и b называется вектор (обозначается a ´ b или [ab]), по величине равный площади параллелограмма, построенного на векторах a и b, перпендикулярный плоскости этих векторов и направленный в такую сторону, чтобы вращение от a к b кратчайшим путем вокруг полученного вектора происходило в ту же сторону, как вращение орта e1 до совмещения с ортом e2 вокруг орта e3 используемого базиса.
Из определения векторного произведения сразу следует, что оно его не коммутативно и что
a ´ b = – b ´ a.В левой координатной системе направление
векторного произведения противоположно направлению векторного произведения тех же векторов в правой координатной системе.Поэтому такой вектор называют псевдовектором или аксиальным вектором, в отличие от истинного, или полярного вектора, направление которого не меняется при переходе от правой системе координат к левой или наоборот.
Модуль векторного произведения
c = a ´ b по определению равен произведению модулей векторов и синуса угла a между ними:|c| = |a|
×|b|×sina.Векторное произведение коллинеарных векторов равно нулю.
Векторное произведение обладает свойством дистрибутивности
| d = a ´ (b + с) = a ´ b + a ´ с. | (7) |
Для доказательства разложим векторы
b и с по составляющим, параллельным и перпендикулярным вектору a:b = ma + b¢; c = na + c¢;
их сумма предстанет в виде
b
+ с = (m + n) a + (b¢ + c¢).Легко убедиться, что
| a ´ b = a ´ b¢, | (8) |
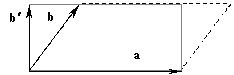
поскольку площадь параллелограмма, построенного на векторах
a и b, равна площади прямоугольника, построенного на векторах a и b¢. Аналогично| a ´ c = a ´ c¢; a ´ (b + с) = a ´ (b¢ + с¢). | (9) |
Остается показать, что
| a ´ (b¢ + с¢) = a ´ b¢ + a ´ с¢. | (10) |
Плоскость рисунка перпендикулярна вектору
a, поэтому в ней лежат векторы b¢, с¢ и b¢ + с¢.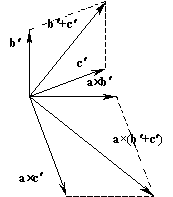
В этой же плоскости должны лежать и векторные произведения a ´ b¢, a ´ c¢, a ´ (b¢ + с¢), перпендикулярные вектору a, а также векторам b¢, с¢ и b¢ + с¢ соответственно. Таким образом, параллелограмм, построенный на векторах a ´ b¢ и a ´ c¢, подобен параллелограмму, построенному на векторах b¢ и с¢, он повернут на 90°, а длины его сторон и изображенная диагональ в a раз больше. Эти диагональ равна a ´ (b¢ + c¢), так что приходим к равенству (10), а от него с учетом равенств (8) и (9) – к соотношению (7).
Всякую площадку S можно изобразить вектором, длина которого равна ее площади, а направление совпадает с направлением нормали к площадке. Поскольку нормаль можно провести в две противоположные стороны, на ограничивающем площадку контуре нужно задать направление обхода, которое определит направление положительной нормали n к площадке.
Положительной нормалью к площадке называется единичный вектор, перпендикулярный площадке и направленный от нее в ту сторону, откуда обход по контуру кажется совершающимся против (в правой системе координат) часовой стрелки.
Проекция площадки S, изображаемой вектором S = S n, на какую-либо плоскость P, может быть изображена вектором, являющимся проекцией вектора S на перпендикуляр к плоскости P.
Доказательство
Пусть плоскости S и P составляют угол a. Обозначим линию их пересечения через KK¢ .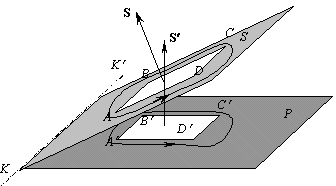
Рассмотрим прямоугольник ABCD, две стороны которого AB и CD параллельны прямой KK¢ , а две другие BC и AD перпендикулярны KK¢ .
Этот прямоугольник спроецируется в прямоугольник A¢ B¢ C¢ D¢ на плоскости P, две стороны которого A¢ B¢ =C¢ D¢ будут равны сторонам AB = CD, две другие будут иметь длину
A¢ D¢ =B¢ C¢ = AD
cos a = BC cos a.Поэтому площадь четырехугольника
DS проектируется в площадь DS¢ =DS cos a четырехугольника A¢ B¢ C¢ D¢ . Т. к. площадь S можно составить из большого числа достаточно малых прямоугольников вида ABCD с такой же их ориентацией, как ABCD, проекция S¢ всей площади S равна S¢ =S cos a.С другой стороны, проекция вектора
S на перпендикуляр к плоскости P имеет длину S cos a, и, рассматриваемая как вектор, является положительной нормалью для S¢ . Следовательно, S¢ может быть представлена проекцией вектора S на нормаль к P, что и требовалось доказать.Вектором может быть представлена не только площадка, но и многогранная поверхность.
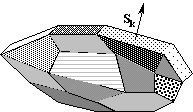
Приведем в соответствие каждой грани этой поверхности изображающий ее вектор
S1, S2, … Sn,
причем направление положительного обхода каждой грани определяем из направления обхода всей многогранной поверхности S. Сумму векторов S = S1 + S2 + … + Sn будем считать вектором, представляющим нашу многогранную поверхность. Если поверхность замкнута, то
S = S1 + S2 + … + Sn = 0.
Это следует из рассмотренного доказательства для проекции вектора площади.
Докажем это утверждение сначала для произвольного тетраэдра. Спроектируем его на какую-нибудь плоскость, например, XY. В проекции мы получим четырехугольный или треугольный контур. Каждый треугольник проекции представляется вектором, направленным по положительной или отрицательной оси Z, смотря по тому, составляет ли внешняя нормаль к той грани, проекция которой рассматривается, с осью Z острый или тупой угол.
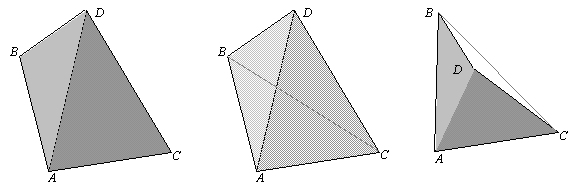
В случае четырехугольного контура проекции (средний рисунок) грани ABD и ACD представляются векторами, направленными вдоль оси Z (к нам), а грани ABC и BCD – против оси Z (от нас). Длина вектора, являющегося суммой векторов проекций граней ABD и ACD на плоскость XY, равна площади четырехугольника ABDC, а направление вектора – вдоль оси Z. Длина же вектора, являющегося суммой векторов проекций граней ABC и BCD на плоскость XY, тоже равна площади четырехугольника ABDC, но направление вектора – против оси Z, так что сумма всех векторов проекций равна нулю. Точно также доказывается случай треугольного контура проекции (правый рисунок).
Итак, проекция вектора площади тетраэдра на плоскость XY равна нулю. Т. к. плоскостью XY может служить любая плоскость, проекция вектора площади тетраэдра на любую плоскость равна нулю. Следовательно, равен нулю и сам вектор площади.
Любой многогранник может быть мысленно разбит на ряд тетраэдров. Внутренние грани такого составного многогранника будут принадлежать двум смежным тетраэдрам, и будут представлены парами одинаковых по величине противоположно направленных векторов, которые при суммировании дадут нуль. Таким образом, вектор площади многогранника равен сумме векторов площадей тетраэдров, а поскольку последние равны нулю, равна нулю и площадь многогранника.
Мы можем иметь дело и с кривой поверхностью. Зададим на ней направление обхода и определим представляющий эту поверхность вектор следующим образом. Впишем в данную поверхность многогранную поверхность с очень малыми гранями, определим для нее представляющий ее вектор и перейдем к пределу, разбивая грани на более мелкие так, чтобы самая крупная из них стягивалась в точку. Полученный вектор и называется вектором данной поверхности. Из только что доказанного следует, что вектор площади всякой замкнутой поверхности равен нулю.
Полученный результат допускает простую физическую интерпретацию. Рассмотрим несжимаемую жидкость, находящуюся в покое, на которую не действуют внешние силы. По закону Паскаля гидростатическое давление p в ней всюду одно и то же. Выделим в жидкости произвольный объем V, ограниченный поверхностью SV. На малый участок поверхности DS этого объема действует сила гидростатического давления, направленная против его внешней нормали: , DF = – p DS. Полная сила, действующая на объем V, складывается из сил давления по всей поверхности объема и равна
![]()
Здесь суммирование ведется по всей поверхности
SV, ограничивающей объем V. Поскольку в равновесии полная сила, действующая на объем V, должна быть равна нулю, то и вектор поверхности SV должен быть равен нулю.Рассмотрим векторные произведения ортов. Из определения векторного произведения следует:
| (11) |
| (12) |
векторное произведение
a´ b с помощью этих соотношений может быть выражено через компоненты векторов и орты в виде определителя: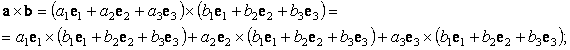
используем сначала соотношения (11)
![]()
затем соотношения (12):
![]()
теперь перегруппируем:
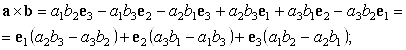
в последнем соотношении нетрудно увидеть определитель
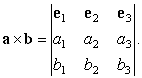
Примерами практического применения векторного произведения в физике являются момент импульса
L = r ´ p, момент силы M = r ´ F, скорость точек твердого тела, вращающегося около некоторой оси. В статике доказывается, что силу, приложенную к твердому телу, можно, не изменяя ее действия на твердое тело, переносить вдоль линии ее действия (иными словами, сила, приложенная к твердому телу, есть передвижной вектор). Докажем, что при таком переносе силы не меняется момент силы.Обозначим новый радиус-вектор посредством
r¢ ; разность векторов r¢ – r есть вектор перемещения силы вдоль линии ее действия и потому коллинеарен ей: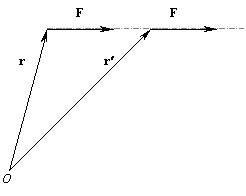
r¢ – r =
l F; r¢ = r + l F.Новый момент силы
M¢
= r¢ ´ F= (r + l F) ´ F = (r ´ F) + l(F ´ F) = r ´ F = Mравен прежнему.
Момент относительно некоторой точки
O (выберем ее за начало отсчета) равнодействующей двух сил F1 и F2, приложенных в одной и той же точке, равен сумме моментов этих сил:r ´
(F1 + F2) = r ´ F1 + r ´ F2.Если к твердому телу приложено несколько сил, геометрическая сумма этих сил
R
= F1 + F2 + …Fnназывается главным вектором сил.
Геометрическая сумма моментов этих сил относительно точки
O называется главным моментом системы сил относительно точки O: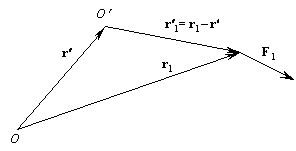
M = r1´ F1 + r2´ F2 + …rn´ Fn,
где
r1, r2, …rn – радиус-векторы точек приложения сил F1, F2, …Fn относительно точки O. Если рассмотреть момент сил относительно другой точки O¢ с радиус-вектором r¢ , радиус-векторы точек приложения сил F1, F2, …Fn относительно точки O¢ равныr¢
1 = r1 – r¢ ;r¢ 2 = r2 – r¢ ;
… … …
r¢ n = rn – r¢ .
Поэтому
| M¢ = r¢ 1´ F1 + r¢ 2´ F2 + … + r¢ n´ Fn = | |
| =(r1 – r¢ )´ F1 + (r2 – r¢ )´ F2 + … + (rn – r¢ )´ Fn = | |
| = (r1´ F1 + r2´ F2 + … + rn´ Fn) – r¢ ´ (F1 + F2 + … + Fn) = M – (r¢ ´ R). | (13) |
Если главный вектор сил
R = 0, то M¢ =M, главный момент сил относительно любой точки одинаков; если r ¹ 0, то главный момент сил относительно любой точки определяется по формуле (13). Скалярное произведение M× R есть величина постоянная в любом случае: т. к. r ^ (r¢ ´ R),M× R = M ¢ × R + (r¢ ´ R )× R = M¢ × R.
Главный вектор
R и скалярное произведение M× R называются статическими инвариантами системы, потому что они не зависят от выбора точки O.Другое важное приложение векторного произведения – в выражении для вектора скорости точек твердого тела, вращающегося около некоторой оси.
Пусть твердое тело вращается около оси
OA. Возьмем какую-нибудь точку M твердого тела. При вращении она описывает окружность в плоскости, перпендикулярной оси вращения OA, ее центр лежит на оси OA.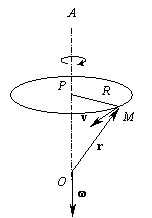
За время
Dt радиус R=PM повернется на угол Dq и пройдет путь R× Dq. Скорость точки M определится пределом отношения пройденного пути ко времени![]()
и будет направлена по перпендикуляру к
PM. Величина![]()
называется угловой скоростью вращения тела.
Отложим от точки
O вектор w, равный по величине w и направленный по прямой OA туда, откуда вращение кажется совершающимся против часовой стрелки, если выбрана правая система координат. Назовем этот вектор вектором угловой скорости. Из рисунка видно, что![]()
Аналогично угловой скорости определяется вектор угла: отложим от точки
O вектор q, равный по величине q и направленный по прямой OA туда, откуда вращение кажется совершающимся против часовой стрелки, если выбрана правая система координат. Этот вектор и называется вектором угла. При бесконечно малом повороте перемещение
| dl = dq ´ r | (14) |
Если твердое тело принимает участие одновременно в нескольких вращениях около разных осей, проходящих через одну и ту же точку
O, с разными угловыми скоростями w1, w2, … , wn, каждому вращению будет отвечать составная скорость точки Mv1 = w1´ r, v2 = w2´ r, … , vn = wn´ r,
и т. к. скорость составного движения равна геометрической сумме скоростей составляющих движений, то
v = v1 + v2 + … + vn =
w1´ r +w2´ r + … + wn´ r = (w1 + w2 + … + wn) ´ r = w ´ r,где
w
= w1 + w2 + … + wn.