
Предисловие
Для просмотра рекомендуется использовать Internet Explorer, т.к. именно этот браузер позволяет корректно воспроизводить использованные в тексте шрифты типа Symbol. Netscape® Communicator 4.6 не отображает корректно эти шрифты. Другие версии Netscape® Communicator не проверялись.
Для определения векторов применяют два подхода – первый основан на наглядной геометрической интерпретации и применим только в нашем привычном трехмерном пространстве. Второй – координатный – является абстрактным математическим и имеет значительно более широкую применимость.
Сначала используем первый подход. Определим первым делом скаляр.
Скаляром называется величина, характеризующаяся при выбранной единице меры одним числом Два скаляра одинаковой размерности равны, если при измерении их одной и той же единицей меры получаются одинаковые числа.
Вектором называется величина, характеризующаяся, помимо измеряющего ее в определенных единицах меры числа, еще своим направлением в пространстве.
Каждому вектору можно сопоставить прямолинейный отрезок, имеющий направление рассматриваемого вектора и длину, равную численному значению вектора и отложенную в некотором масштабе.
Два вектора, обладающие одной и той же размерностью, равны, если они имеют одно и то же направление и одинаковое численное значение при использовании одной и той же единицы меры.
Отметим, что различают векторы трех типов: свободные
, перемещаемые и определенные векторы. У определенных векторов точка приложения должна быть зафиксирована.У перемещаемых векторов точку приложения можно произвольно перемещать вдоль самого вектора.
В физике приходится иметь дело еще с другими величинами, тоже направленного характера, но более сложного, чем векторы, строения. Эти величины называются тензорами. Их определение будет дано позднее. Так, например, распределение моментов инерции относительно различных осей, проходящих через заданную точку твердого тела, приводит к понятию тензора моментов инерции; распределение напряжений на различно направленные элементы поверхности в некоторой точке упругого тела приводит к понятию тензора упругих напряжений, и др.
Для векторов определены правила сложения, вычитания, скалярного умножения и векторного умножения.
Сложение векторов осуществляют с помощью правила параллелограмма
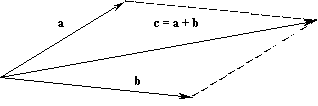
или треугольника:
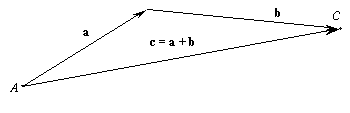
тогда чтобы получить вектор c, представляющий собой сумму двух векторов a и b, надо от произвольной точки A пространства отложить вектор a, к концу его приложить начало вектора
b и соединить точку A с концом C вектора b, тогда ![]() по величине и направлению представляет вектор c.
по величине и направлению представляет вектор c.
Из правила параллелограмма очевидно, что сложение коммутативно
:a + b = b + a
Чтобы образовать сумму трех векторов
a, b и c (лежащих или не лежащих в одной плоскости), сначала складывают векторы a и b, и к результирующему вектору прибавляют вектор c:d = (a + b) + c.
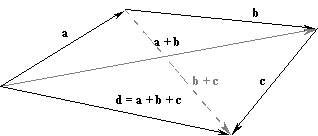
Из рисунка видно, что тот же результат получается, если к первому вектору прибавить сумму второго и третьего, следовательно,
d =
(a + b) + c = a + (b+c),т. е. сложение векторов обладает ассоциативностью
.Умножение на скаляр l > 0 дает вектор
b = la, имеющий то же направление, что и вектор a, но длину в l раз большую. Умножение на скаляр l < 0 дает вектор b = la, имеющий направление, противоположное вектору a, и длину в l раз большую длины вектора a . В обоих случаях векторы a и b параллельны друг другу. Такие векторы называют коллинеарными. Важен случай, когда один из коллинеарных векторов имеет длину, равную единице. Такие векторы называют единичными векторами или ортами. Орты будем обозначать буквой e. Любой коллинеарный ему вектор a можно представить в видеa
= ae.Очевидна справедливость формул
(m + n)a = ma + na;
m(na) = (mn)a = n(ma).
Если векторы
a и b умножить на скаляр l и затем сложить, то получится результат, одинаковый с тем, который мы получили бы, сначала сложив векторы a и b, а затем умножив сумму на скаляр l:la + lb = l(a + b).
В этом выражается дистрибутивный закон умножения вектора на скаляр.
Если l
= –1, то b = – a, т. е. b + a = 0, и вычитание векторов a – b можно представить в виде суммы векторов a + (–1×b).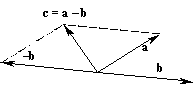
Если векторы
a и b не коллинеарны, то вектор| c = ma + nb | (1) |
параллелен плоскости, определяемой векторами
a и b, поскольку геометрическая сумма векторов, лежащих в одной плоскости, лежит в той же плоскости. Векторы, параллельные одной плоскости, называют компланарными. Всякий вектор c, компланарный векторам a и b, может быть представлен формулой (1). Для доказательства отложим векторы a, b и c от одной точки O и проведем через конец вектора c прямые, параллельные векторам a и b.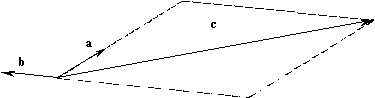
Они пересекутся с прямыми, проходящими через векторы
a и b. Тогда вектор c представится как сумма векторов, коллинеарных векторам a и b и поэтому допускающих представление в виде ma и nb. Тем самым утверждение доказано. Представление вектора c формулой (1) единственно. Действительно, если бы существовали такие m¢ ¹ m и n¢ ¹ n, чтоc
= ma + nb;и одновременно
c
= m¢a + n¢b,то, вычитая из первого равенства второе
0 = (m – m¢) a + (n – n¢) b,
мы получили бы
![]()
а это равенство означает, что векторы
a и b коллинеарны Это противоречит принятому допущению. Они не коллинеарны, только если m = m¢ и n = n¢. Отсюда следует единственность разложения вектора c по векторам a и b.Аналогично, если три вектора
a, b и c не компланарны, всякий вектор d может быть представлен в форме| d = ma + nb + pc, | (2) |
т. е. может быть разложен по трем не компланарным векторам
a, b и c. Доказательство аналогично предыдущему. Проводим через конец вектора d плоскости, параллельные граням трехгранного угла, образованного векторами a, b и c. Они совместно с гранями трехгранного угла образуют параллелепипед с ребрами, параллельными векторам a, b и c.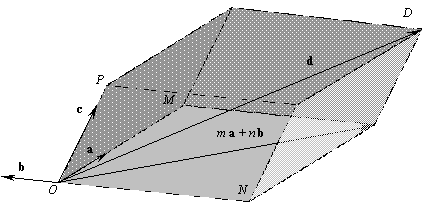
Вектор
![]()
равен сумме векторов, коллинеарных векторам
a, b и c, и потому может быть представлен в форме (2). Аналогично предыдущему доказывается и единственность этого разложения.Скалярное, или внутреннее произведение тесно связано с понятием проекции одного вектора на другой. По определению,
a ×b
= |a| ×|b| ×cos a,где a
– угол между векторами a и b. Но ab = |a| ×cos a есть проекция вектора a на направление вектора b,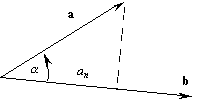
т. е. расстояние, измеряемое в направлении вектора
b от общей точки начала этих двух векторов до основания перпендикуляра, опущенного из конца вектора a на прямую, проходящую вдоль вектора b. Это расстояние положительно, если cos a > 0. Иногда под проекцией понимают не просто расстояние (с учетом знака), но и направление, т. е. считают проекцию вектором. Скалярное произведение можно представить в равноценных формах| a ×b = |a| ×|b| ×cos a = ab×|b| = |a| ×ba. | (3) |
Очевидно,
a ×b
= b ×a, a ×(b + c) = a ×b + a ×c,т. е. скалярное произведение коммутативно и дистрибутивно.
Проекция геометрической суммы векторов на какое-либо направлениеu равна алгебраической сумме проекций слагаемых векторов на то же направление:
(a + b + … + d)u = au + bu + … + du.
Достаточно доказать это утверждение для двух векторов
c = a + b:| (a + b)u = au + bu, | (4) |
т. к. один из них может быть суммой других векторов.
Из рисунка видно, что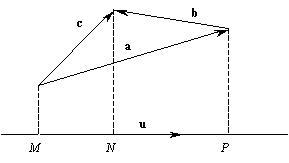
![]()
Но
Таким образом, мы пришли к соотношению (4).
Ранее мы видели, что всякий вектор может быть разложен по трем некомпланарным векторам a, b и c. Возьмем в качестве векторов a, b и c взаимно перпендикулярные орты e1, e2, e3 и назовем их базисом связанной с ними координатной системы. Соотношение (2) может быть переписано в виде
| d = d1e1 + d2e2 + d3e3. | (5) |
Проекции
d1, d2, d3 вектора d на координатные оси – прямые, проходящие через орты – называются прямоугольными координатами, или составляющими, или компонентами вектора d. Если обозначить углы между вектором d и ортами посредством q1, q2, q3, тоd
1 = d cosq1; d2 = d cosq2; d3 = d cosq3.Эти косинусы называют направляющими косинусами вектора
d. Обозначим их для краткости буквами a, b, g. Имеем:| (6) |
Возможны два типа базисов
e1, e2, e3: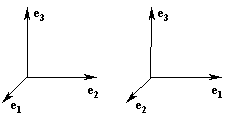
Если смотреть вдоль вектора
e3, то кратчайшим будет поворот вектора e1 до совмещения с вектором e2 в первом случае по часовой стрелке, во втором – против. Координатная система, связанная с первым базисом, называется правой. Если направить отставленный большой палец правой руки по направлению вектора e3, то остальные полусогнутые пальцы укажут направление поворота вектора e1 до совмещения с вектором e2 в правой системе координат. Координатная система, связанная со вторым базисом, называется левой.Если два вектора равны между собой, то равны друг другу их соответствующие компоненты, и наоборот:
если
a = b, то a1 = b1; a2 = b2; a3 = b3. Это непосредственно следует из единственности разложения вектора по не-компланарным направлениям.
Компоненты суммы векторов равны суммам компонент слагаемых: если
u = a + b + c + …,
то
ui = ai + bi + ci + … .
Это следует из доказанного утверждения, что проекция геометрической суммы векторов на какое-либо направление равна алгебраической сумме проекций слагаемых векторов на то же направление.